The worker/wrapper transformation is a technique for transforming a computation of one type into a worker of a different type, together with a wrapper that acts as an impedance matcher between the original and new computations. The technique can be used to improve the performance of functional programs by improving the choice of data structures used.

Transformation Overview

(click to enlarge)

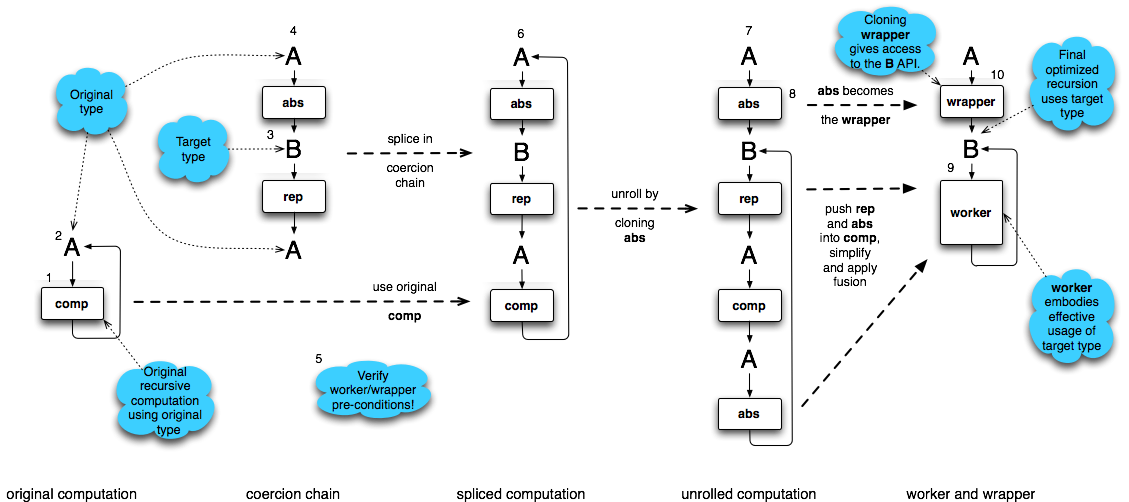
This image is an abstract diagram explaining the worker/wrapper transformation, where arrows signify usage. The (smaller) boxes are computations that have a type, given as an incoming arrow on the left hand side, and require the use of a second computation, given as an outgoing arrow on the right hand side. These computational boxes can be considered representing functions with higher-order arguments. A and B should be read as providing a typed service by using the box to their right to provide this service.

The original computation is a recursive function, that is it uses itself, notated with a right arrow that arcs back to the type of the computation, A. The ultimate result is a wrapper and an optimized worker, which operates using a new type, B.

The worker/wrapper transformation operates as follows:

  1. A target type for the recursion is selected, called B.
  2. A coercion chain is constructed from two higher-order functions that coerce from A to B, and back to A.
  3. The worker/wrapper local preconditions are verified; one example is when abs and rep form an identity.
  4. The worker/wrapper transformation is applied, replacing then the original computation with the post worker/wrapper chain.
  5. This new formulation can be transformed and optimized using well understood local refinements into a worker that operates efficiently over B, and a wrapper abs that allows original users of A to call this new function.

This general pattern captures many possible transformations and refinements.

Worker/Wrapper Theorem

The transformation can be expressed formally, using the theory of least fixed points over pointed ω-complete partial orders (the semantic domain of Haskell).

Worker/Wrapper Factorization Rule

If comp :: A is defined by comp = fix body for some body :: A→A, and rep :: A→B and abs :: B→A satisfy any of the worker/wrapper assumptions, then

comp = abs work

where work :: B is defined by

work = fix (rep ο body ο abs)

Alternatively, work can be defined as

work = rep comp

which avoids the need to define comp using an explicit fixed point.

Worker/Wrapper Assumptions

There are several worker/wrapper assumptions that are sufficient to justify worker/wrapper factorization. The three given in the worker/wrapper paper are:

    | Rule                                   | Rule Name --------|----------------------------------------|----------------------------- **(A)** | **abs ο rep = id**                     | (basic assumption) **(B)** | **abs ο rep ο body = body**            |(body assumption) **(C)** | **fix (abs ο rep ο body) = fix body**  |(fixed-point assumption)

There is also another possible assumption, which uses the fixed point fusion rule (hence the name fpf assumption) and only holds for a strict abs:

(D) wrap ο rep ο body ο abs = body ο abs (fpf assumption) ——- —————————————- —————–

Worker/Wrapper Fusion Rule

If any of the worker/wrapper assumptions (A), (B) or (C) hold, then:

rep (abs work) = work

Papers

Use Cases

The Worker/Wrapper Transformation is surprisingly general! It has been applied to the following application areas:

  • Using strictness information—was the original motivating example for this transformation.
  • CPS translation—is just using an alternative representation for computation.
  • Memoization—is using a data-structure to represent a function.
  • Accumulation—is often possible when the result is a monoid; worker/wrapper enables this change of type.
  • Constructor specialization—creates specialized workers and wrappers.
  • Cross-function short-cut fusion—uses worker/wrapper to transmit fusion opportunities over function boundaries.

We expect there are many others.