Constrained Type-Class Problem
In Haskell, there are many data types that could be made instances of standard type
classes such as Functor and Monad, were it not for the presence of type-class
constraints on the operations on that data type.
This is a frustrating problem in practice, because there is a considerable amount of support and infrastructure for standard type classes that these data types cannot use.
We call this the Constrained-Type-Class Problem.
To give a concrete example, the abstract type Set provided by the Data.Set module cannot be made an instance of the Monad type class, because of Ord constraints on operations over Set.
One significant occurrence of the constrained-type-class problem is when embedding a Domain-Specific Language (DSL) in Haskell, where it is necessary to restrict the types that can appear in an embedded computation so that the computation can be compiled to some other language. This restriction can prevent type classes with polymorphic methods being used to structure such computations.
Existing Solutions
There have been numerous solutions suggested to address the constrained-type-class problem. John Hughes proposed a language extension for Restricted Data Types: data types with attached class constraints on their parameters. In the same paper he also proposed Restricted Type Classes: type classes that take a class constraint as an additional parameter. Several simulations of restricted type classes were implemented, such as in the RMonad library, before the arrival of the Constraint-Kinds GHC extension, which enabled them to be encoded directly.
However, these solutions all require modifying existing type classes (or adding new ones), so do not allow for interoperability with infrastructure and libraries that use the existing classes in their current form. An alternative approach is to modify the data type such that the desired class instance can be declared, in such a way that class operations applied to this new data type can be interpreted in the same way as the desired class operations on the original data type.
Normalized Computations
This can be achieved by embedding the original data type (which we call the type of primitive operations) in a new data type that represents a normal form of computations constructed using the operations of the type class over the primitive operations.
What is required from a normal form is that all types introduced by polymorphic class methods should appear either as type parameters on primitive operations, or as top-level type parameters of the computation.
Any other types should be eliminated when converting to the normal form.
For example, the normal form for monadic computations consists of a sequence of right-nested >>=s, terminating in a return:
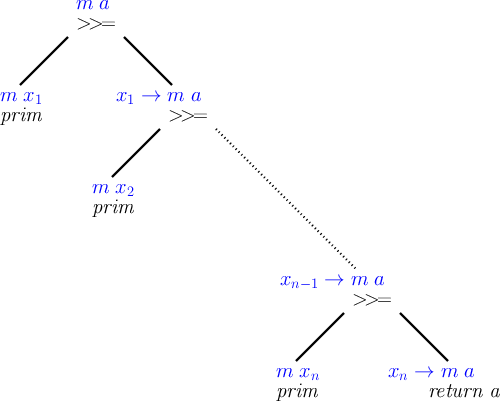
One way to convert a computation to this normal form is to use a continuation transformer, as demonstrated by Persson et al. Another way is to construct a deep embedding of the computation, and restructure that deep embedding into the normal form by applying the monad laws as rewrites. This latter approach is how the AsMonad transformer from the RMonad library is implemented, and is also used by Unimo and Operational, albeit for a different purpose.
We are currently investigating the normalized deep-embedding technique. This technique is not limited to monads, and is applicable to any type class for which a normal form can be defined that contains no types other than those that appear as parameters on primitive operations, or as the top-level parameters of the computation.
Publications and Libraries
N. Sculthorpe, J. Bracker, G. Giorgidze, and A. Gill, “The constrained-monad problem,” in Proceedings of the 18th ACM SIGPLAN International Conference on Functional Programming, pp. 287–298, ACM, 2013.